В дальнейшем Архимед, используя метод верхних и нижних приближений, получает следующие границы числа пи:
Индусы в V-VI веках пользовались числом
,китайцы- числом
"Письменная история числа p начинается с египетского папируса,
датируемого примерно 2000 годом до нашей эры, но оно было известно
еще древним людям. Число p обратило на себя внимание людей ещё в те
времена, когда они не умели письменно излагать ни своих знаний, ни
своих переживаний, ни своих воспоминаний. С тех пор как первые
натуральные числа 1,2,3,4,… стали неразлучными спутниками
человеческой мысли, помогая оценивать количества предметов
либо их длины, площади или объёмы, люди познакомились с числом p.
Тогда оно ещё не обозначалось одной из букв греческого алфавита и
его роль играло число 3. Нетрудно понять, почему числу p уделяли
так много внимания. Выражая величину отношения между длиной окружности
и её диаметром, оно появилось во всех расчётах связанных с площадью
круга или длиной окружности". Но уже в глубокой древности математики
довольно быстро и не без удивления обнаружили, что число 3 не совсем
точно выражает то, что теперь известно как число пи. Безусловно, к
такому выводу могли прийти только после того, как к ряду натуральных
чисел добавились дробные или рациональные числа. Так египтяне получили
результат:
В дальнейшем Архимед, используя метод верхних и нижних приближений,
получает следующие границы числа пи:
Индусы в V-VI веках пользовались числом
,
китайцы- числом
"Обозначение числа p происходит от греческого слова
("окружность"). Впервые это обозначение использовал в 1706 году
английский математик У.Джонс, но общепринятым оно стало после того,
как его (начиная с 1736 года) стал систематически употреблять Леонард
Эйлер".
В конце 18 века И.Ламберт и А.Лежандр установили, что p иррациональное
число, а в 1882 году Ф.Лидерман доказал, что оно трансцендентное, т.е.
не может удовлетворять никакому алгебраическому уравнению с целыми
коэффициентами.
На протяжении всего существования числа p, вплоть до наших дней,
велась своеобразная "погоня" за десятичными
знаками числа p.
Леонардо Фибоначи около 1220 года определил три первых точных десятичных знаков числа p.
В 16 веке Андриан Антонис определил 6 таких знаков. Франсуа Виет (подобно Архимеду), вычисляя периметры вписанного и описанного 322216-угольников, получил 9 точных десятичных знаков. Андриан Ван Ромен таким же способом получил 15 десятичных знаков, вычисляя периметры 1073741824-угольников. Лудольф Ван Кёлен, вычисляя периметры 32512254720-угольников, получил 20 точных десятичных знаков. Авраам Шарп получил 72 точных десятичных знаков числа p.
В 1844 году З.Дазе вычисляет 200 знаков после запятой числа p,
в 1847 году Т.Клаузен получает 248 знаков, в1853 Рихтер вычисляет 330 знаков, в том же 1853 году 440 знаков получает З.Дазе и в этом же году У.Шенкс получает 513 знаков.
"С появлением ЭВМ количество верных знаков десятичных знаков резко возрастает:
При вычислении верных десятичных знаков числа p пользовались различными способами, некоторые, как и Архимед вычисляли периметры вписанных и описанных n-угольников, но позднее стали прибегать к помощи рядов. Так Лейбниц вычислял с помощью ряда:
Шарп применил ряд:
Л.Эйлер с помощью ряда:
З.Дазе использовал ряд:
Джон Валлис (1616-1703) нашёл бесконечное произведение, с помощью которого можно вычислить число пи:
Теорема:Отношение длины окружности к её диаметру одинаково для всех окружностей.
Доказательство.
Обозначим через L — длину окружности, через d — её диаметр, то формулировка теоремы запишется следующим образом:
Рассмотрим правильный n-угольник, вписанный в окружность радиуса r со стороной аn и периметром Рn, то
Докажем, что отношение
одинаково для всех окружностей. Рассмотрим две произвольные окружности с вписанными в них правильными n-угольниками.
Из подобия треугольников АОВ и А1О1В1 следует, что
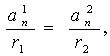
т.к. окружности брали произвольные, то это равенство будет справедливо для всех окружностей.
Итак,
для всех окружностей, следовательно
Это отношение длины окружности к её диаметру принято обозначать греческой буквой "p".
Определение: Числом p называется отношение длины окружности к её диаметру.
